Why Helicopters Reach Their Limits in High Mountains

If you've ever wondered why rescue operations in high mountains can't "just use helicopters," while camera drones apparently have no problem with altitude - I wondered the same thing and did some research to break it down for those interested:

Diagram: Maximum RPM vs. Rotor Diameter

The Fundamental Problem: Thin Air

The thinner air at altitude reduces lift equally for both drones and helicopters, in principle.

You can compensate for this with higher drive power / higher rotor speed.

The Transonic Barrier

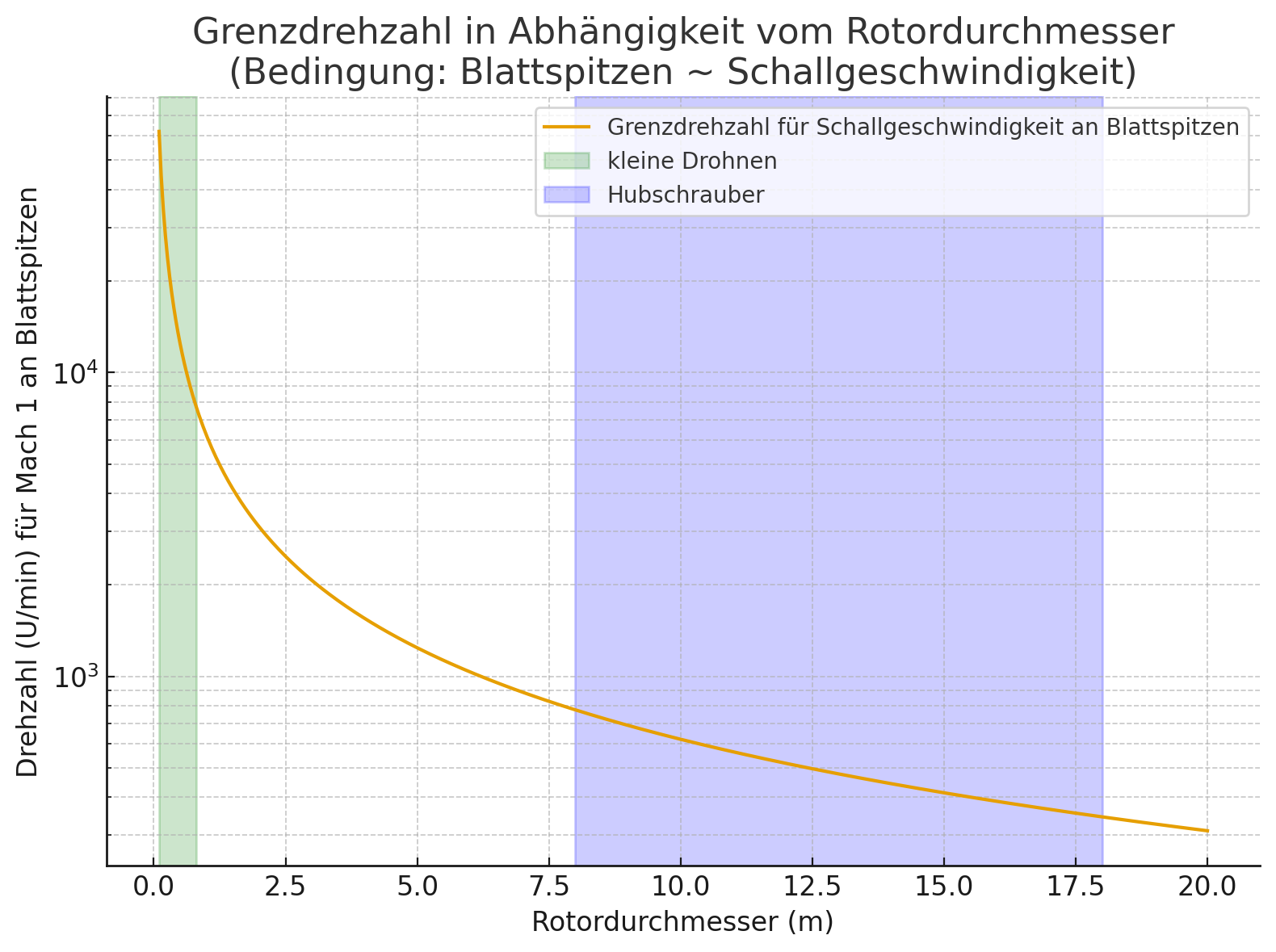
However, this hits a hard limit at the point where the rotor blade tips would reach the speed of sound.

The "transonic drag" causes the power required for higher speeds to spike dramatically, and the generated lift even decreases again due to flow separation.

This point is reached at considerably lower rotational speeds for larger rotor diameters due to the "leverage effect."

The Mathematics Behind It

The velocity at the blade tip naturally increases linearly with rotor diameter:

V_{tip} = π \times D \times \frac{n}{60}

D := Diameter
n := Rotational speed in RPM

When we substitute Mach 1 and rearrange:

n [RPM] = \frac{343 m/s \times 60 s/min}{π \times D [m]}

Why Drones Still Manage

The small camera drone can simply compensate with absurd propeller speeds (accepting very high power consumption). The helicopter cannot do this.

In practice, the limit is around 4000 - 6000 m above sea level, depending on weather and helicopter type.

Individual records up to 7000 m.

Why Not Just Use Smaller Rotors?

So should we simply build helicopters with smaller rotors for high-altitude rescue?

Unfortunately, that doesn't work. The thrust T of a rotor is approximately:

T = 2 \times ρ \times A \times v^{2}

ρ := Air density (linear factor, so helicopter and drone equally affected)

A = π \times {(\frac{D}{2})}^{2}

:= Rotor area
(Note: diameter is squared here)
v := Jet velocity through the disk
(we'll skip the exact derivation, but rotational speed is squared in there)

The Quadratic Problem

We thus have quadratically better lift with increasing rotor diameter at constant v.

So if we have a fixed required lift, we CANNOT simply replace one rotor with area A by two rotors with A/2 - we need more...

Conclusion

→ A helicopter would need numerous smaller rotors to replace one large one, resulting in quite a monstrosity.

The laws of physics are clear here: Large rotors are more efficient for heavy loads, but due to the transonic barrier they cannot spin fast enough at high altitude. Small rotors can spin faster, but due to the quadratic relationship between diameter and lift, they require an impractically large number of units.

That's why lightweight camera drones work at extreme altitudes, while rescue helicopters hit their physical limits.